Many thanks to Jed Duersch for discussion of these concepts and contributions to this post.
Sometimes the term sparse is used to refer to a matrix that has a large fraction of missing entries, but the more typical usage of that term is to refer to a matrix that has a large fraction of zero entries.
Unfortunately, these concepts are often conflated for a variety of reasons. For instance, a common technique for replacing missing entries is to replace them by zeros. Assuming the data is centered, i.e., has mean zero, this may be a reasonable approach in some situations. Conversely, zeros are sometimes used as indicators of missingness, though this makes it impossible to identify known zeros and is not recommended!
We want to develop terminology and approaches for real-world data where both zeros and missing entries can be prevalent, and we need to be able to sort out which is which as well as store the information efficiently.
For the purposes of this discussion, we have matrices of size $m \times n$ with $p$ known nonzero entries, $q$ known zero entries, and $r$ unknown/missing entries. Necessarily, $p+q+r=mn$. We use the notation $\cong$ to indicate being approximately the same size and the notation $\ll$ to indicate at least one order of magnitude smaller.
Dense Matrices with No Missing Data
If the matrix is dense and has no missing entries, we store it the usual way, i.e., in an array of length $mn$ with an explicit value for each entry.
- Storage for matrix: $mn$
- Storage for location of missing entries: N/A
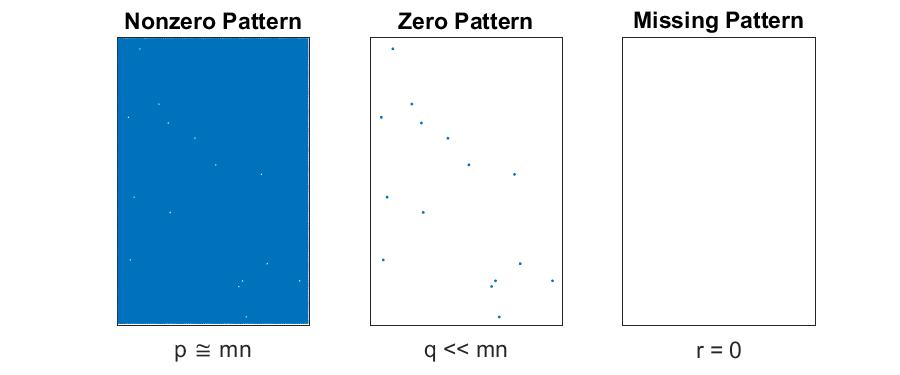
Dense Matrices with Some Missing Data
If the matrix is dense and has a few missing entries, we store it the usual way, i.e., in an array of length $mn$ with an explicit value for each entry. The missing entries can be any value, but we recommend zero since it’s convenient for certain computations that are common in such a scenario. We have to separately store the pattern of missing entries. We could store the locations as an array or hash table, but in this case it is just as easy to store it as a dense 0-1 indicator matrix.
- Storage for matrix: $mn$
- Storage for location of missing entries: $mn$
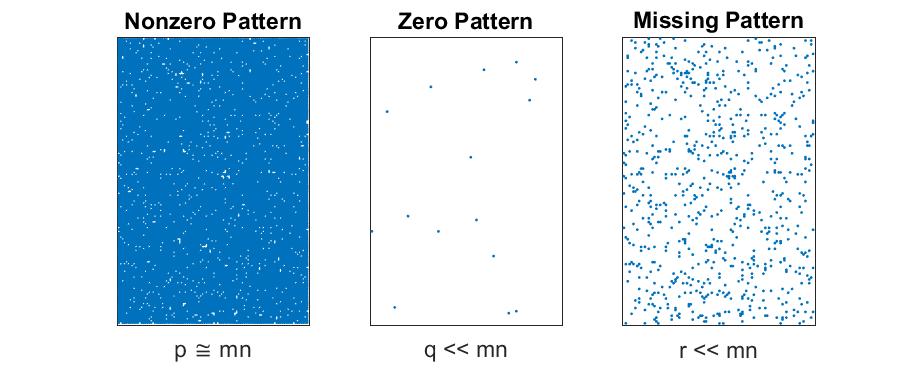
Sparse Matrices with No Missing Data
We say that matrix is sparse if $p \ll mn$. In this case, it’s more efficient to store and operate only only the $p$ nonzeros and their locations rather than explicitly storing the zeros. Implicit elements are defined to be zero, and we can infer the locations of the $q \cong mn$ zero entries from the locations of the nonzeros.
- Storage for matrix: $\mathcal{O}(p)$
- Storage for location of missing entries: N/A
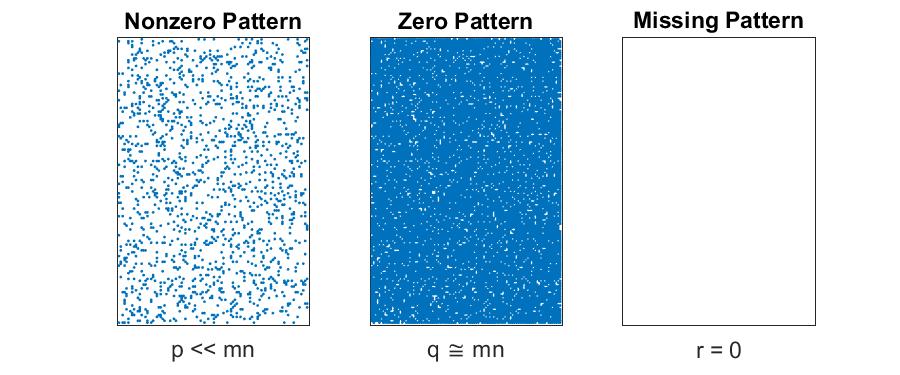
Scarce Matrices
I propose to use the term scarce if $p+q \ll mn$. That is, in the case that very few entries are known (and some of them may be zero). The relationship between $p$ and $q$ is irrelevant to the storage in this case. We store the $p+q$ known entries and their locations, requiring $\mathcal{O}(p+q)$ storage. The (few) zeros are stored explicitly. Implicit entries are defined to be unknown, and we can infer the locations of the $r \cong mn$ missing entries from the locations of the known entries.
- Storage for matrix: $\mathcal{O}(p+q)$
- Storage for location of missing entries: 0
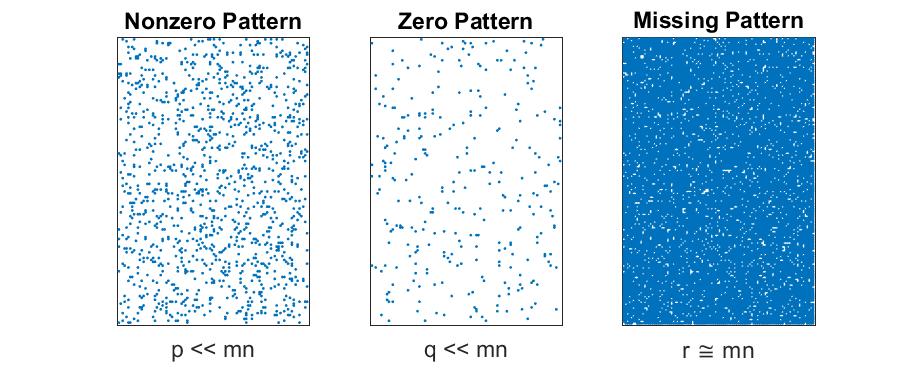
Sparse Matrices with Some Missing Data
This isn’t scarce since the majority of entries are known, but just happen to be mostly zeros. In this case, $p+r \ll mn$. We can separately store the $p$ nonzero entries and their locations and the $r$ missing locations, using a total of $\mathcal{O}(p+r)$ storage. The known zeros are stored implicitly, and we infer the locations of the known zeros from the locations of the known nonzero and missing entries.
- Storage for matrix: $\mathcal{O}(p)$
- Storage for location of missing entries: $\mathcal{O}( r )$
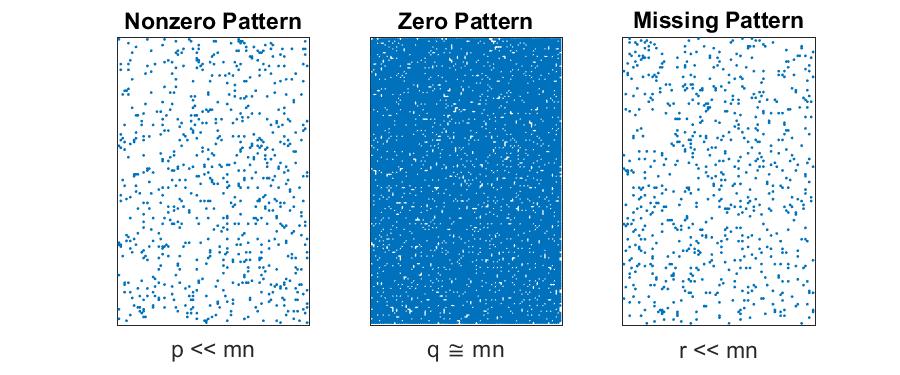
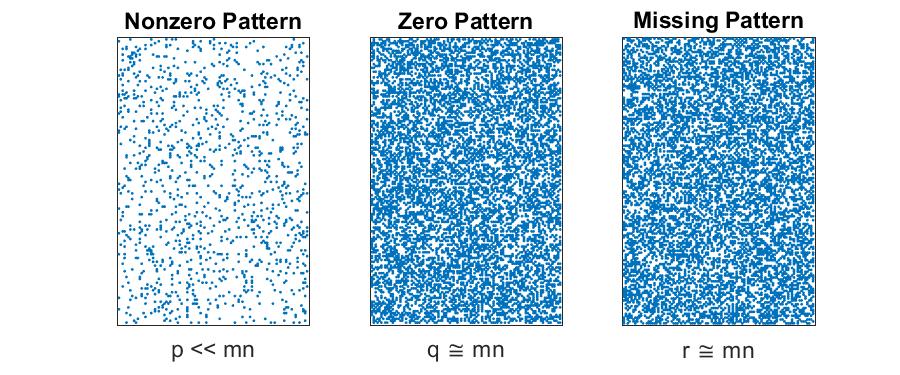
Sparse with Mix of Known Zeros and Missing Data
If $p \ll mn$ but $q \cong mn$ and $r \cong mn$, then we have a difficult situation. In order to track the pattern of missing data, we require $mn$ storage. In this case, it’s probably best just to revert to the “Dense Matrices with Some Missing Data” case. However, it is possible to save space by storing the nonzeros and their locations along with a compressed binary indicator matrix. We can get 32-64X compression simply packing the binary entries rather than storing them as regular integers or doubles. If there is some pattern to the missingness (like every third entry is missing), then that’s another way to achieve compression. But generally there is no efficient way to handle this situation.
Use Cases
Exactly how the missing data is to be incoporated may impact the data structures.
Mask. In some cases, the locations of missing entries may need to be masked to zero so that they are omitted from a computation. In this case, we would ideally have a 0/1 matrix that is efficient to multiply with.
Selection. In other cases, we need to select randomly amongst the known entries. This is used, for instance, in stochastic gradient descent. We may need to be able to quickly determine if a selected entry is missing so that we can do rejection sampling. This entails usage of efficient data structures such as hash tables.
Commentary: How Sparse is Sparse?
I usually recommend that a matrix should not be considered sparse unless fewer than 10% of its entries are nonzero. Even if the storage is reduced by using a sparse representation, the computations are much less efficient and so dense storage is often preferable. It’s only when the storage savings is an order of magnitude or more that a sparse representation makes sense.
What About Tensors?
Of course, all of this discussion applies to tensors as well! That’s really what I’m interested in after all. That’s really how this discussion came about.
Closing Comments
Please email me with any thoughts or suggestions at tgkolda@sandia.gov or @TammyKolda